5.2 Propiedades de las Realciones
Reflexiva e Irreflexiva
Una relación R en un conjunto A es reflexiva si (a, a) £ R para todas las a £ A, esto es, si a R e para todas las a e A. Una relación R en un conjunto A es irreflexiva si a R a para toda a £ A.
Por consiguiente, R es reflexiva si cada elemento a e A está relacionado consigo mismo y es irreflexiva si ningún elemento está relacionado consigo mismo.
Ejemplo 1:
(a) Sea Δ = [(a, a)\ a £ A], de modo que A es la relación de igualdad en el conjunto A. Entonces A es reflexiva, ya que (a, a) £ Δ para todas las a e A.
(b) Sea R = {(a, b) e A x A | a + b}, R es la relación de desigualdad en el conjunto A. Entonces R es irreflexible, ya que (a, a) £ R para todas las x € A.
(c) Sean A = {1, 2, 3}. y Jí = {(1, 1), (1, 2)}. Entonces A es reflexiva ya
(2,2) R y (.3,3) € R. Por otra parte, R no es irreflexiva, ya que (1, l) € R.
(d) Sea A un conjunto no vacio. Sea R = Ǿ A x A, la relación vacía. Enlaces R no es reflexiva, ya que (a, a) € R para todas las a € A (el conjunto vacío tiene elementos). Sin embargo, R es irreflexiva.
Simétrica y Asimétrica
Una relación R en un conjunto A es simétrica si cuando a R b, entonces b R a. De esto se sigue que R no es simétrica se tiene a y b € A con a R b, pero b R a. Una relación R en un conjunto A es asimétrica si cuando a R b, entonces b Ra. De esto se sigue que R no es simétrica si se tiene a y b e A con ambos a R b y b R a.
Una relación R en un conjunto A es asimétrica si cuando a R b y b R a, entonces a = b. Otra forma de expresar esta definición es diciendo que R es anti simétrica si cuando a ≠ b, se tiene a R b o b R a. De esto se sigue que R no es anti simétrica si se tiene a y b en A. a ≠ b, y ambas a R b y b R a.
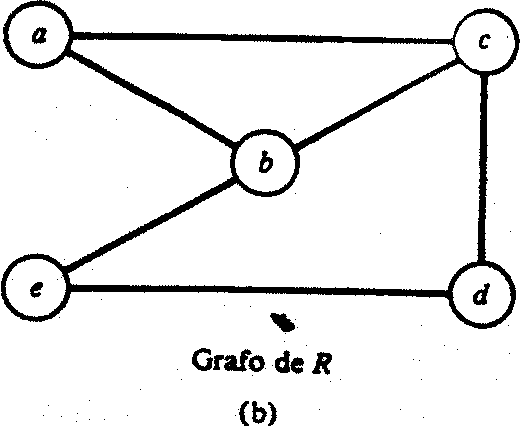
Ejemplo Sea A «= [a, b, c, d, e} y sea R la relación simétrica dada por
R = {(a, b), (b, a), (a, c), (c, a), (b, c), (c, b), (b, e), (e, b), (e, a), (a, e), (c,a), (a,c)}
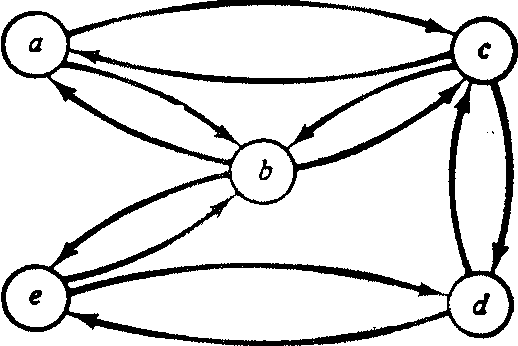
El grafo dirigido de R se muestra en la figura 2(a), mientras que en la figura
Grafo dirigido de R Grafo dirigido de R
Aparece el grado de R. Obsérvese que cada arista no dirigida corresponde a dos pares ordenados en la relación R.
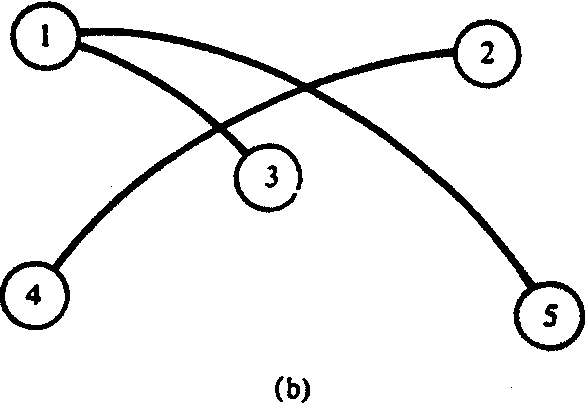
A una relación simétrica R en un conjunto A se le llamará conexa si existe una trayectoria de cualquier elemento de A a cualquier otro elemento de A. Esto significa sencillamente que el grafo de R está todo en una pieza. En la figura 3 se muestran los grafos de dos relaciones simétricas. El grafo de la figura 3(a) está conectado mientras que el de la figura 3(b) no lo está.
Transitiva
BIBLIOGRAFIA:
Libros:
Matemáticas discretas – con aplicación a las ciencias de la computación
JEAN-PAUL TREMBLAY
ISBN: 0-070605142-6
Matemáticas discretas
RICHARD JOHNSONBAUGH
ISBN: 0-02-360720-3
Matemáticas discretas-sexta edición
RICHARD JOHNSONBAUGH
PEARSON EDUCACIÓN, México, 2005
ISBN: 970-26-0637-3
Área: Universitarios
Formato: 21 x 27 cm paginas 696
Se dice que una relación R en un conjunto A es transitiva si cuando a R b y b R e, entonces a R c. Se sigue que R no es transitiva si y sólo si se puede encontrar elemento a, b y c en A tal que a R b y b R c, pero a R c.
Ejemplo: Sea A = Z el conjunto de los enteros y sea R la relación considerada en el ejemplo 2 Para ver si R es transitiva, se supone que a R b y b R c. Por consiguiente, a < b; b < c. Entonces se sigue que a < c, por lo cual a R c. De aquí que R sea transitiva.
Una relación R en un conjunto A es transitiva si y sólo si satisface las siguientes propiedades: Si existe una trayectoria de longitud mayor que 1 del vértice a al vértice b, hay una trayectoria de extensión 1 de a a b (esto es, a está relacionada con b). Establecido algebraicamente, R es transitiva si y sólo si Rn £ R para todas las n ≥ 1.
Es posible caracterizar la relación transitiva por su matriz MR = [mij] así:
si mij =1 y mjk = 1, entonces mik = 1
Para ver qué significa transitividad en términos del grafo dirigido de una relación, se traducirá esta definición a términos geométricos.
Si se examinan los vértices particulares a y c, las condiciones a R b y b R c
ocurrirán si y sólo si existe una trayectoria de longitud 2 de a a c, esto es, si y sólo si a R2 c. Es posible replantear la definición de transitividad como sigue: Si a R2 c, entonces a R c, esto es, R2 £ R (como un subconjunto de A x A).