Concepto de Proposición

La lógica proposicional es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad. En la Lógica proposicional las proposiciones no se analizan, sino que se toman como un bloque y son los elementos mínimos sobre los cuales opera esta rama de la Lógica.

 

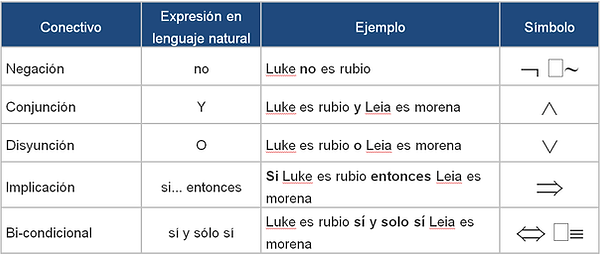
Una proposición es una oración enunciativa, es decir, que afirma o niega algo y que por lo tanto, puede ser verdadera o falsa. Esta proposición será representada por las Variables Proposicionales o Letras Enunciativas que corresponden a letras del alfabeto latino, empezando por la letra p, luego q, r, s, etc.

 

Una proposición es una sentencia simple, también conocida como Proposición Simple, que tiene un valor asociado ya sea verdadero (V), o falso (F). Por ejemplo:

·      hoy _es _sábado

·     hace _frío

 

 

 

 

Proposiciones Compuestas

 

Las proposiciones pueden combinarse para expresar conceptos más complejos, esto es conocido como Proposición Compleja o Compuesta, en la cual se unen proposiciones simples formando una compleja. Por ejemplo:

·        hoy_es_sábado y hace_frío.

 

Cada una de estas afirmaciones es verdadera en condiciones diferentes. Dichas condiciones vienen dadas por las distintas conectivas lógicas.

 

En la lógica proposicional, los conectivos lógicos son tratados como funciones de verdad. Es decir, como funciones que toman conjuntos de valores de verdad y devuelven valores de verdad.

 

 

 

 

 

 

 

 

 

 

 

 

Los conectivos lógicos son funciones que permiten combinar valores de verdad y entregar valores de verdad, esto se puede visualizar mediante una tabla que entregue los valores de verdad que la función devuelve con todas las combinaciones posibles.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Tablas de Verdad

Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes. Las tablas de verdad son, por una parte, uno de los métodos más sencillos y conocidos de la lógica formal, pero al mismo tiempo también uno de los más poderosos y claros.

Entender bien las tablas de verdad es, en gran medida, entender bien a la lógica formal misma. En esta sesión haremos algunas reflexiones alrededor de las tablas de verdad cómo pretexto.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Fundamentalmente, una tabla de verdad es un dispositivo para demostrar ciertas propiedades lógicas y semánticas de enunciados del lenguaje natural o de fórmulas del lenguaje del cálculo proposicional:

 - Sin son tautológicas, contradictorias o contingentes

 - Cuáles son sus condiciones de verdad

 - Cuál es su rol inferencia, es decir, cuáles son sus conclusiones lógicas y de qué otras proposiciones se siguen lógicamente

El procedimiento para construir una tabla de verdad es sencillo y relativamente mecánico; en esta plática, asumiré que todos saben ya cómo hacer una tabla de verdad para cualquier fórmula del cálculo proposicional clásico. Para aplicar el método de tablas de verdad a un enunciado o proposición, por lo tanto, es necesario primero simbolizarlo, es decir, determinar qué fórmula del lenguaje proposicional muestra su forma lógica y, luego, elaborar la tabla de verdad de dicha fórmula.

 Si al aplicar el método de tablas de verdad encontramos que una fórmula es tautológica, presumimos que ella es una verdad lógica del cálculo proposicional es decir que es lógicamente válida, lógicamente verdadera o verdadera con necesidad lógica. Por lo tanto, el uso de las tablas de verdad como métodos para demostrar que algo es lógicamente necesario presupone ciertas tesis sobre la verdad y la necesidad lógicas. Cada uno de los pasos y cada una de las características de las tablas de verdad representan una tesis lógica sustancial.

 

 

Tautologías, Contradicción y Contingencia

 

TAUTOLOGÍA: Una proposición compuesta es una tautología si es verdadera para todas las asignaciones de valores de verdad  para sus proposiciones componentes. Dicho de otra forma, su valor V no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso:    A V­­­­­ Ø A

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

•CONTRADICCIÓN: Se entiende por proposición contradictoria, o contradicción, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es F. Dicho de otra forma, su valor F no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso:    A ˄ Ø  A 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

•CONTINGENCIA: Se entiende por verdad contingente, o verdad de hecho, aquella proposición que puede ser verdadera o falsa, (combinación entre tautología y contradicción) según los valores de las proposiciones que la integran. Sea el caso:  A˄ (B VC) 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Equivalencias Lógicas

 

•Definición: Dos formas proposicionales P y Q se dicen lógicamente equivalentes, y se escribe P ≡ Q, si sus tablas de verdad coinciden.

Nota: Esto equivale a decir que P ↔ Q es una tautología; así, P ≡ Q es lo mismo que decir P ⇔ Q.

P → Q ≡~P ∨  Q     – A continuación se muestra en su tabla correspondiente: